چرخ دنده های اپی سیکلیک در چه مواردی استفاده می شوند؟

چرخ‌دنده‌های اپی‌سیکلیهمچنین به عنوان سیستم‌های دنده سیاره‌ای شناخته می‌شوند، به دلیل طراحی جمع و جور، راندمان بالا و تطبیق‌پذیری، به طور گسترده در صنایع مختلف مورد استفاده قرار می‌گیرند.

این چرخ‌دنده‌ها عمدتاً در کاربردهایی استفاده می‌شوند که فضا محدود است، اما گشتاور بالا و تغییرپذیری سرعت ضروری است.

۱. گیربکس‌های خودرو: چرخ‌دنده‌های اپی‌سیکلی یک جزء کلیدی در گیربکس‌های اتوماتیک هستند که تعویض دنده‌های روان، گشتاور بالا در سرعت‌های پایین و انتقال قدرت کارآمد را فراهم می‌کنند.
۲. ماشین‌آلات صنعتی: آنها در ماشین‌آلات سنگین به دلیل توانایی‌شان در تحمل بارهای زیاد، توزیع یکنواخت گشتاور و عملکرد کارآمد در فضاهای فشرده مورد استفاده قرار می‌گیرند.
۳. هوافضا: این چرخ‌دنده‌ها نقش حیاتی در موتورهای هواپیما و روتورهای هلیکوپتر ایفا می‌کنند و قابلیت اطمینان و کنترل دقیق حرکت را در شرایط سخت تضمین می‌کنند.
۴. رباتیک و اتوماسیون: در رباتیک، از چرخ‌دنده‌های اپی‌سیکلی برای دستیابی به کنترل دقیق حرکت، طراحی جمع‌وجور و گشتاور بالا در فضاهای محدود استفاده می‌شود.

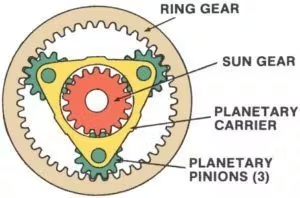
چهار عنصر مجموعه چرخ‌دنده‌های اپی‌سیکلی کدامند؟

یک مجموعه چرخ‌دنده اپی‌سیکلی، که به عنوان ... نیز شناخته می‌شودچرخ دنده سیاره ای سیستم، یک مکانیزم بسیار کارآمد و جمع و جور است که معمولاً در گیربکس‌های خودرو، رباتیک و ماشین‌آلات صنعتی مورد استفاده قرار می‌گیرد. این سیستم از چهار عنصر کلیدی تشکیل شده است:

۱. چرخ دنده خورشیدی: چرخ دنده خورشیدی که در مرکز مجموعه چرخ دنده ها قرار دارد، محرک یا گیرنده اصلی حرکت است. این چرخ دنده مستقیماً با چرخ دنده های سیاره ای درگیر می شود و اغلب به عنوان ورودی یا خروجی سیستم عمل می کند.

۲. چرخ‌دنده‌های سیاره‌ای: اینها چندین چرخ‌دنده هستند که دور چرخ‌دنده خورشیدی می‌چرخند. این چرخ‌دنده‌ها که روی یک حامل سیاره‌ای نصب شده‌اند، هم با چرخ‌دنده خورشیدی و هم با چرخ‌دنده حلقه‌ای درگیر می‌شوند. چرخ‌دنده‌های سیاره‌ای بار را به طور مساوی توزیع می‌کنند و سیستم را قادر به تحمل گشتاور بالا می‌سازند.

3.حامل سیاره: این قطعه چرخ‌دنده‌های سیاره‌ای را در جای خود نگه می‌دارد و از چرخش آنها به دور چرخ‌دنده خورشیدی پشتیبانی می‌کند. حامل سیاره‌ای می‌تواند بسته به پیکربندی سیستم، به عنوان یک عنصر ورودی، خروجی یا ثابت عمل کند.

4.چرخ دنده حلقه ای: این یک چرخ‌دنده بیرونی بزرگ است که چرخ‌دنده‌های سیاره‌ای را احاطه کرده است. دندانه‌های داخلی چرخ‌دنده حلقه‌ای با چرخ‌دنده‌های سیاره‌ای درگیر می‌شوند. مانند سایر عناصر، چرخ‌دنده حلقه‌ای می‌تواند به عنوان ورودی، خروجی یا ثابت عمل کند.

تعامل این چهار عنصر، انعطاف‌پذیری لازم برای دستیابی به نسبت‌های سرعت و تغییرات جهت مختلف در یک ساختار فشرده را فراهم می‌کند.

چگونه نسبت دنده را در یک مجموعه دنده اپی‌سیکلی محاسبه کنیم؟

نسبت دنده یکمجموعه چرخ‌دنده‌های اپی‌سیکلی بستگی به این دارد که کدام اجزا ثابت، ورودی و کدام خروجی باشند. در اینجا یک راهنمای گام به گام برای محاسبه نسبت دنده آمده است:

۱. پیکربندی سیستم را درک کنید:

مشخص کنید کدام عنصر (خورشید، حامل سیاره یا حلقه) ثابت است.

اجزای ورودی و خروجی را تعریف کنید.

۲. از معادله اساسی نسبت دنده استفاده کنید: نسبت دنده یک سیستم دنده اپی‌سیکلی را می‌توان با استفاده از فرمول زیر محاسبه کرد:

GR = 1 + (R / S)

کجا:

GR = نسبت دنده

R = تعداد دندانه‌های چرخ‌دنده حلقه‌ای

S = تعداد دندانه‌های چرخ‌دنده خورشیدی

این معادله زمانی اعمال می‌شود که حامل سیاره‌ای خروجی باشد و یا چرخ‌دنده خورشیدی یا رینگی ثابت باشند.

۳. تنظیم برای سایر تنظیمات:

• اگر دنده خورشیدی ثابت باشد، سرعت خروجی سیستم تحت تأثیر نسبت دنده رینگی و حامل سیاره‌ای قرار می‌گیرد.
• اگر چرخ‌دنده حلقه‌ای ثابت باشد، سرعت خروجی توسط رابطه بین چرخ‌دنده خورشیدی و حامل سیاره‌ای تعیین می‌شود.

۴. نسبت دنده معکوس برای خروجی به ورودی: هنگام محاسبه کاهش سرعت (ورودی بیشتر از خروجی)، این نسبت سرراست است. برای ضرب سرعت (خروجی بیشتر از ورودی)، نسبت محاسبه شده را معکوس کنید.

محاسبه مثال:

فرض کنید یک مجموعه چرخ دنده دارای:

چرخ دنده حلقه ای (راست): ۷۲ دندانه

چرخ دنده خورشیدی (S): ۲۴ دندانه

اگر حامل سیاره‌ای خروجی باشد و دنده خورشیدی ثابت باشد، نسبت دنده عبارت است از:

GR = 1 + (72 / 24) GR = 1 + 3 = 4

این یعنی سرعت خروجی ۴ برابر کندتر از سرعت ورودی خواهد بود و نسبت کاهش ۴:۱ را ارائه می‌دهد.

درک این اصول به مهندسان این امکان را می‌دهد که سیستم‌های کارآمد و همه‌کاره‌ای متناسب با کاربردهای خاص طراحی کنند.